
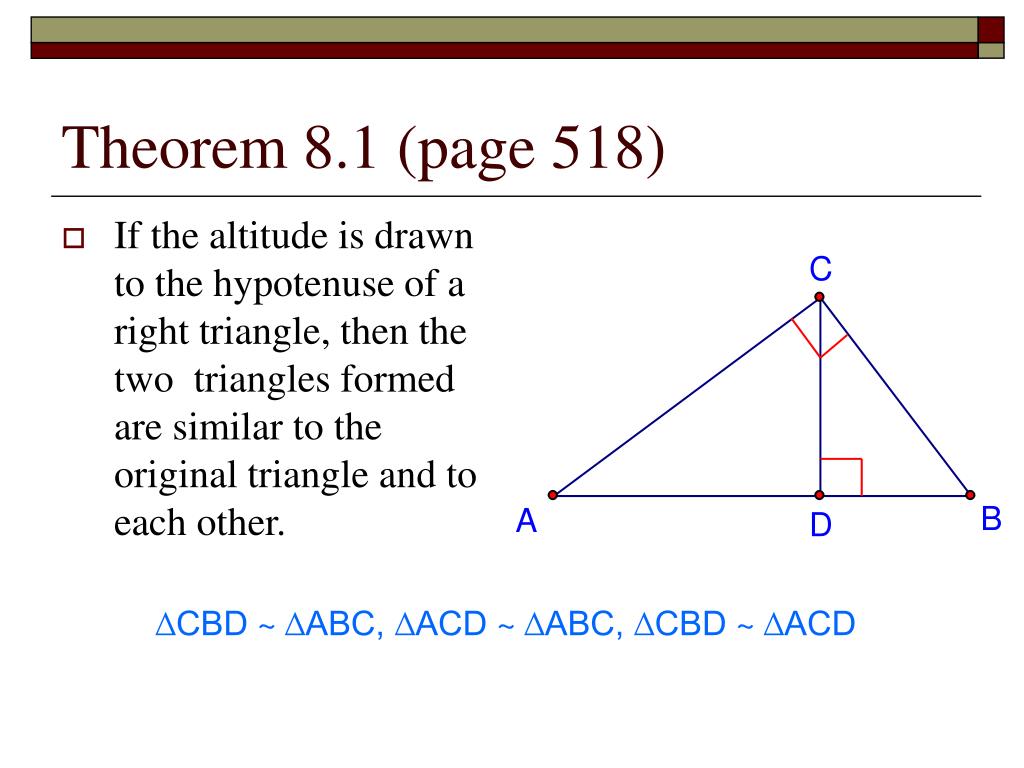
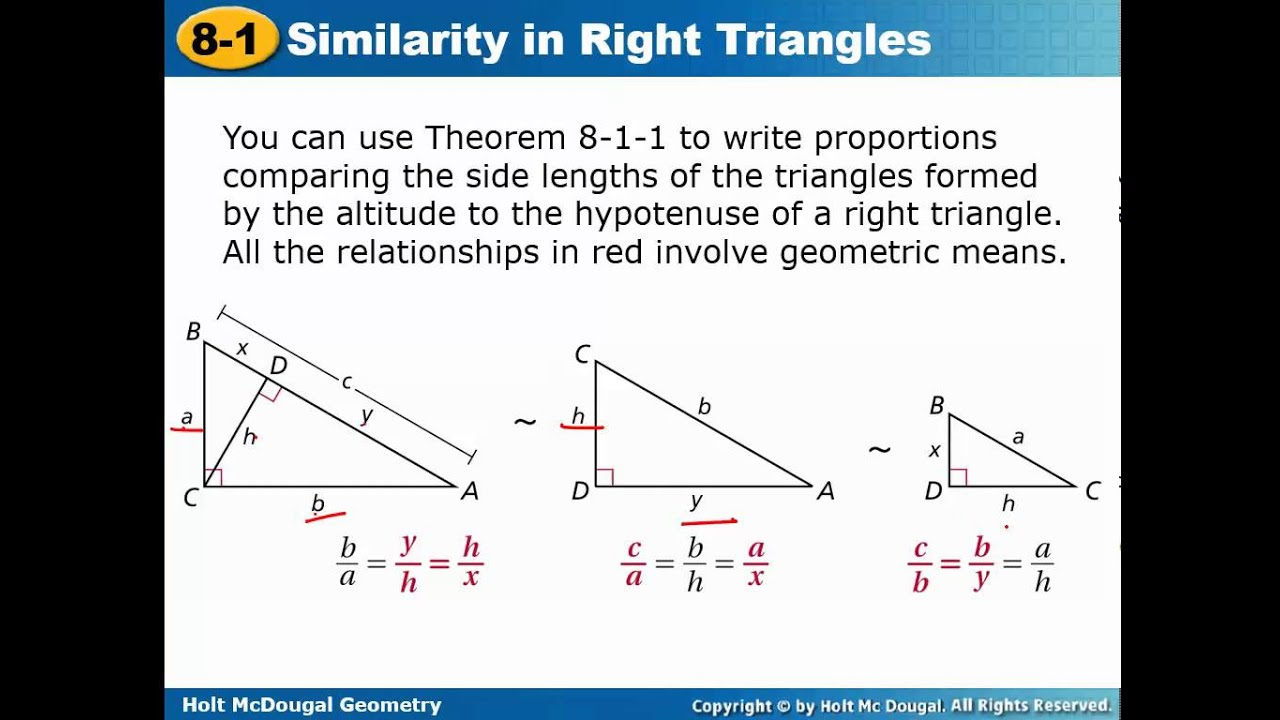
Parts of two triangles can be proportional if two triangles are known to be similar then the perimeters are proportional to the measures of corresponding sides.Ĭontinuing, if two triangles are known to be similar then the measures of the corresponding altitudes are proportional to the corresponding sides. If a line is drawn in a triangle so that it is parallel to one of the sides and it intersects the other two sides then the segments are of proportional lengths: Likewise if the measures of two sides in one triangle are proportional to the corresponding sides in another triangle and the including angles are congruent then the triangles are similar. Theorem 64: If an altitude is drawn to the hypotenuse of a right triangle, then it is the geometric mean between the segments on the hypotenuse.Įxample 1: Use Figure 3 to write three proportions involving geometric means.įigure 3 Using geometric means to write three proportions.Įxample 2: Find the values for x and y in Figures 4 (a) through (d).įigure 4 Using geometric means to find unknown parts.īecause it represents a length, x cannot be negative, so x = 12.If the measures of the corresponding sides of two triangles are proportional then the triangles are similar. In a right triangle, the altitude to the hypotenuse divides it into two right triangles, which are similar to each other and to the given triangle. This proportion can now be stated as a theorem. Theorem 63: If an altitude is drawn to the hypotenuse of a right triangle, then each leg is the geometric mean between the hypotenuse and its touching segment on the hypotenuse. These two proportions can now be stated as a theorem. This produces three proportions involving geometric means. Note that AB and BC are legs of the original right triangle AC is the hypotenuse in the original right triangle BD is the altitude drawn to the hypotenuse AD is the segment on the hypotenuse touching leg AB and DC is the segment on the hypotenuse touching leg BC.īecause the triangles are similar to one another, ratios of all pairs of corresponding sides are equal. They have been drawn in such a way that corresponding parts are easily recognized.įigure 2 Three similar right triangles from Figure (not drawn to scale). Theorem 62: The altitude drawn to the hypotenuse of a right triangle creates two similar right triangles, each similar to the original right triangle and similar to each other.įigure 2 shows the three right triangles created in Figure . The following theorem can now be easily shown using the AA Similarity Postulate. In Figure 1, right triangle ABC has altitude BD drawn to the hypotenuse AC.įigure 1 An altitude drawn to the hypotenuse of a right triangle. Summary of Coordinate Geometry Formulas.In this case, you can prove that two triangles are similar if two of their corresponding angles are equal. Slopes: Parallel and Perpendicular Lines The AA similarity theorem is named after angle angle.Similar Triangles: Perimeters and Areas.Proportional Parts of Similar Triangles.Formulas: Perimeter, Circumference, Area.Proving that Figures Are Parallelograms.Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.
Classifying Triangles by Sides or Angles.Lines: Intersecting, Perpendicular, Parallel.


 0 kommentar(er)
0 kommentar(er)
